2.4 Costs of Production - Class Notes

Contents

• Tuesday, March 23, 2020
• Quarantine Lecture 1

Overview

Today we cover costs and revenues before we put them together next class to solve the firm’s profit maximization problem.

Class Livestream/Lecture Videos

See the above video for a brief overview of Zoom.

• Zoom Live Class Meetings (starts Tuesday 11:30 AM)

Slides

• Lecture Slides

Assignments: Exam 1 Corrections & Homework 3

You will have until the end of the semester (May 4) to turn in your corrections, however, I advise you to do them as soon as possible. See more from the online transition page for details.

Homework 3 is now due, via email, on Sunday, March 29, by 11:59PM. The answer key will be posted Monday, March 30.

Appendix

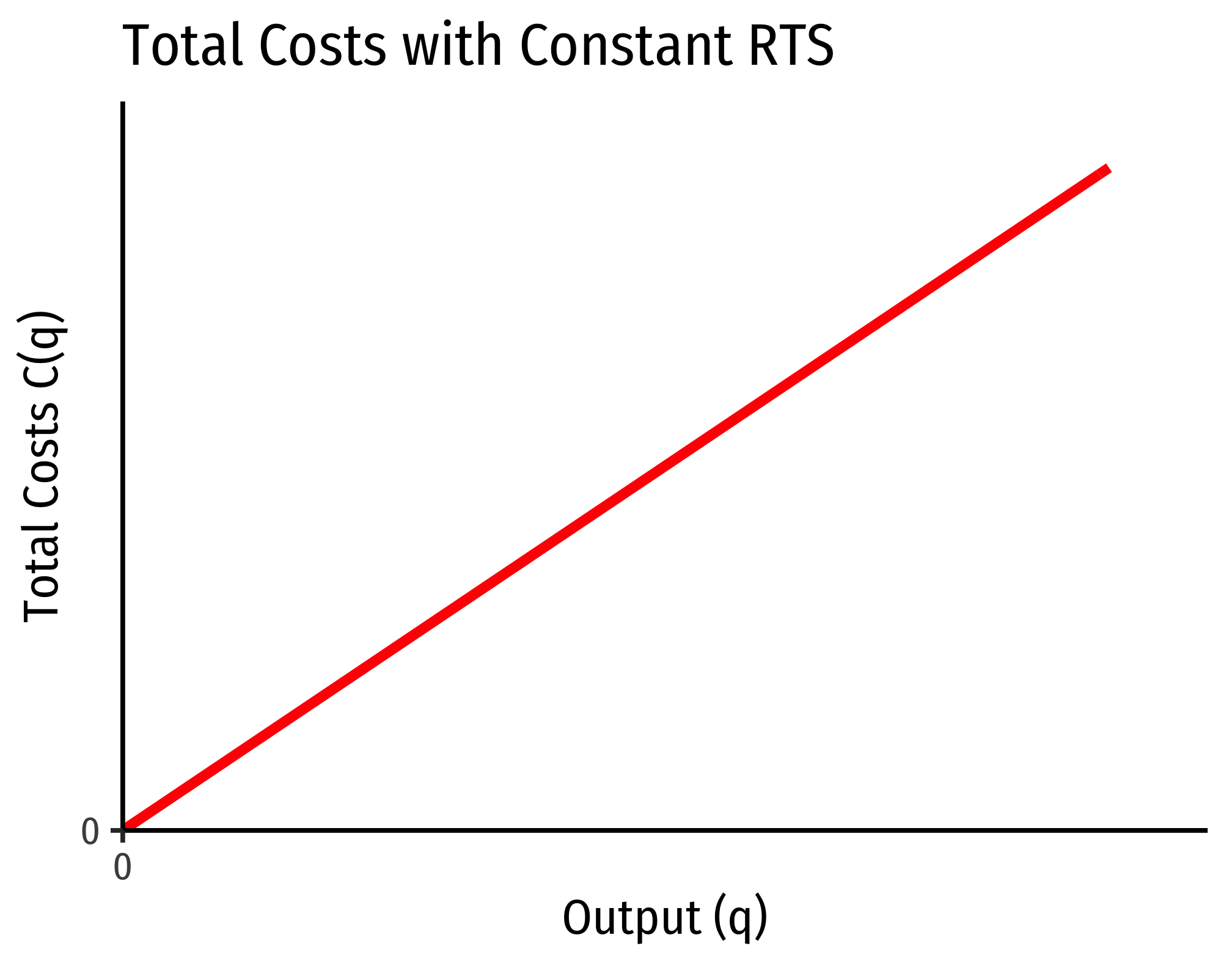
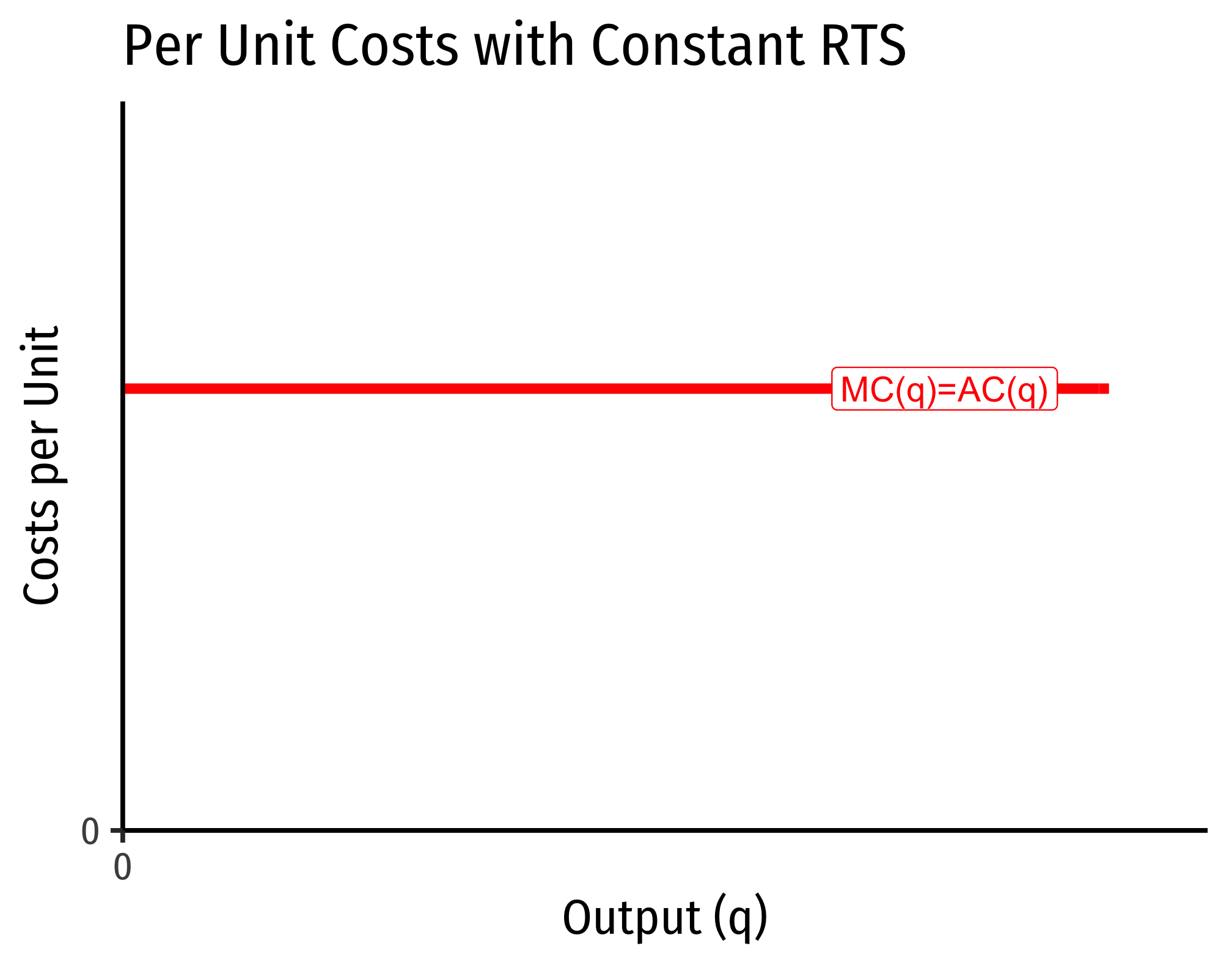
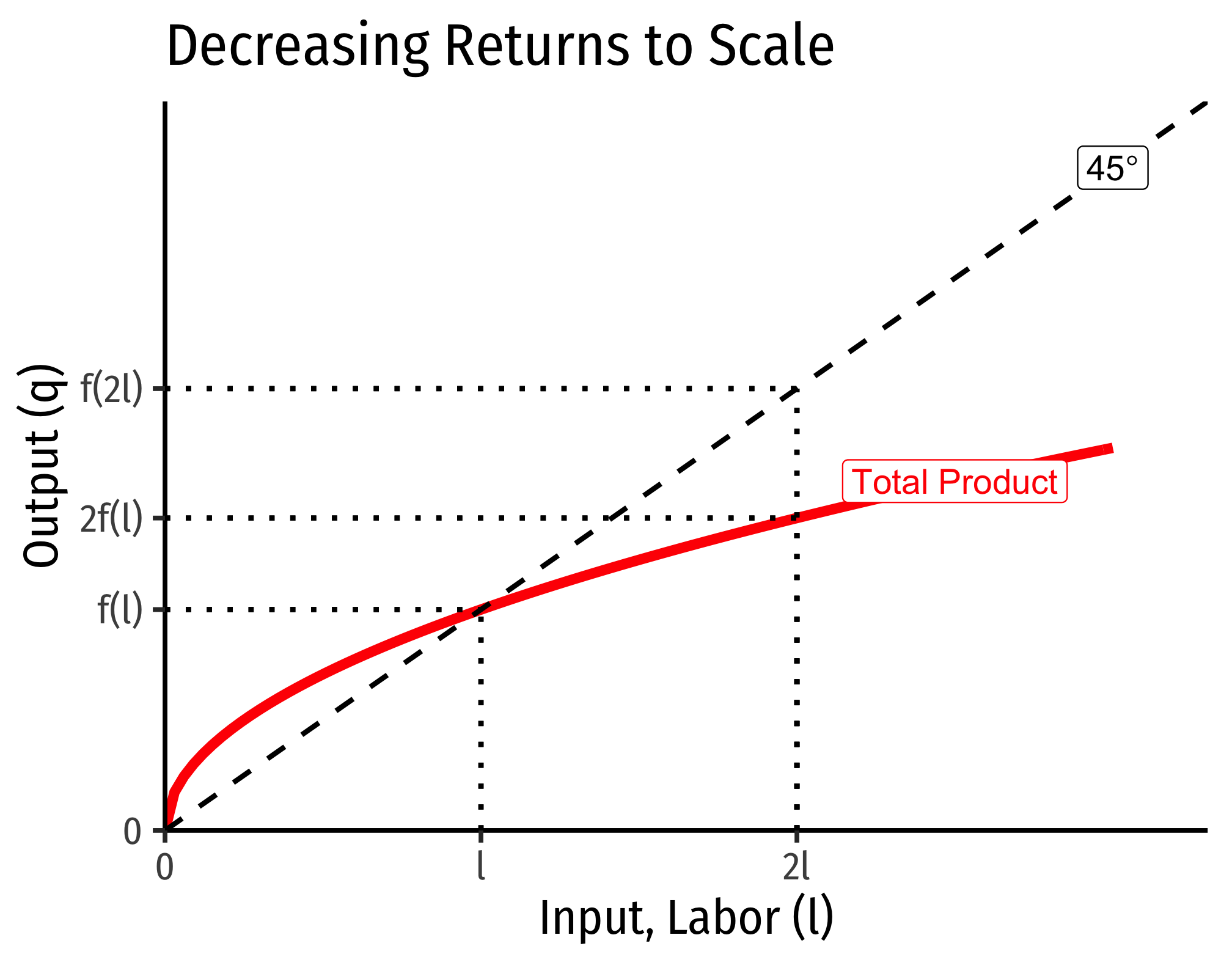
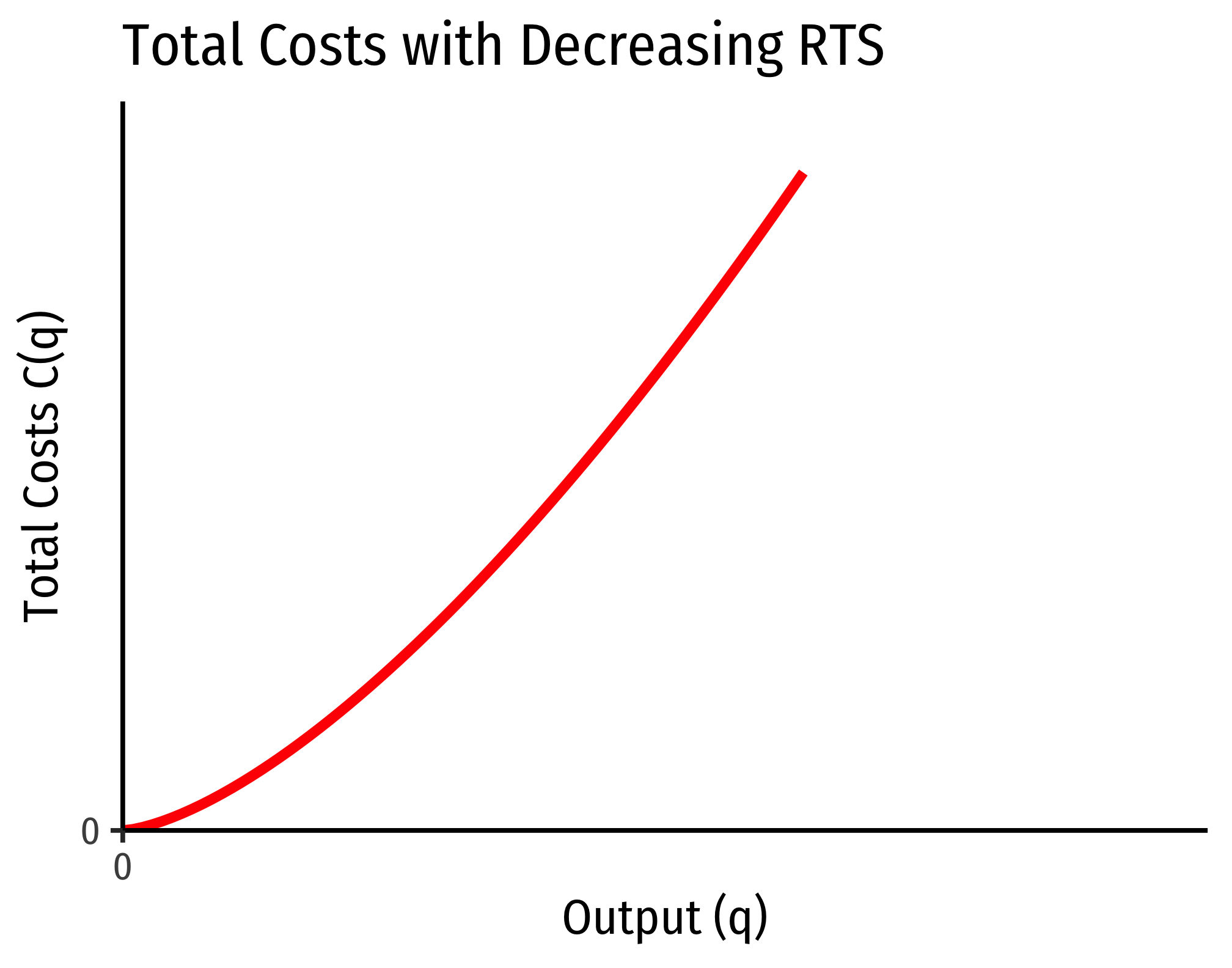
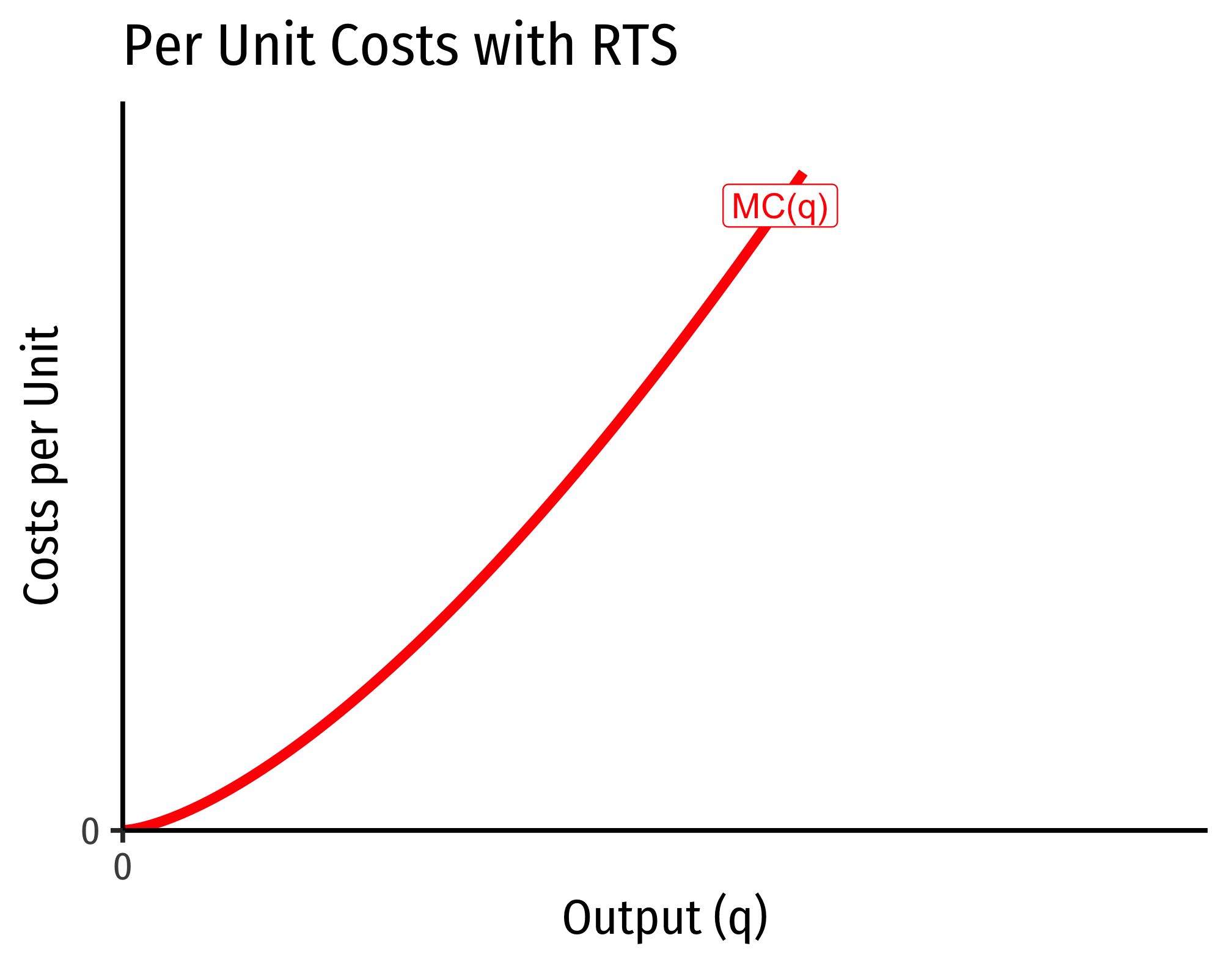
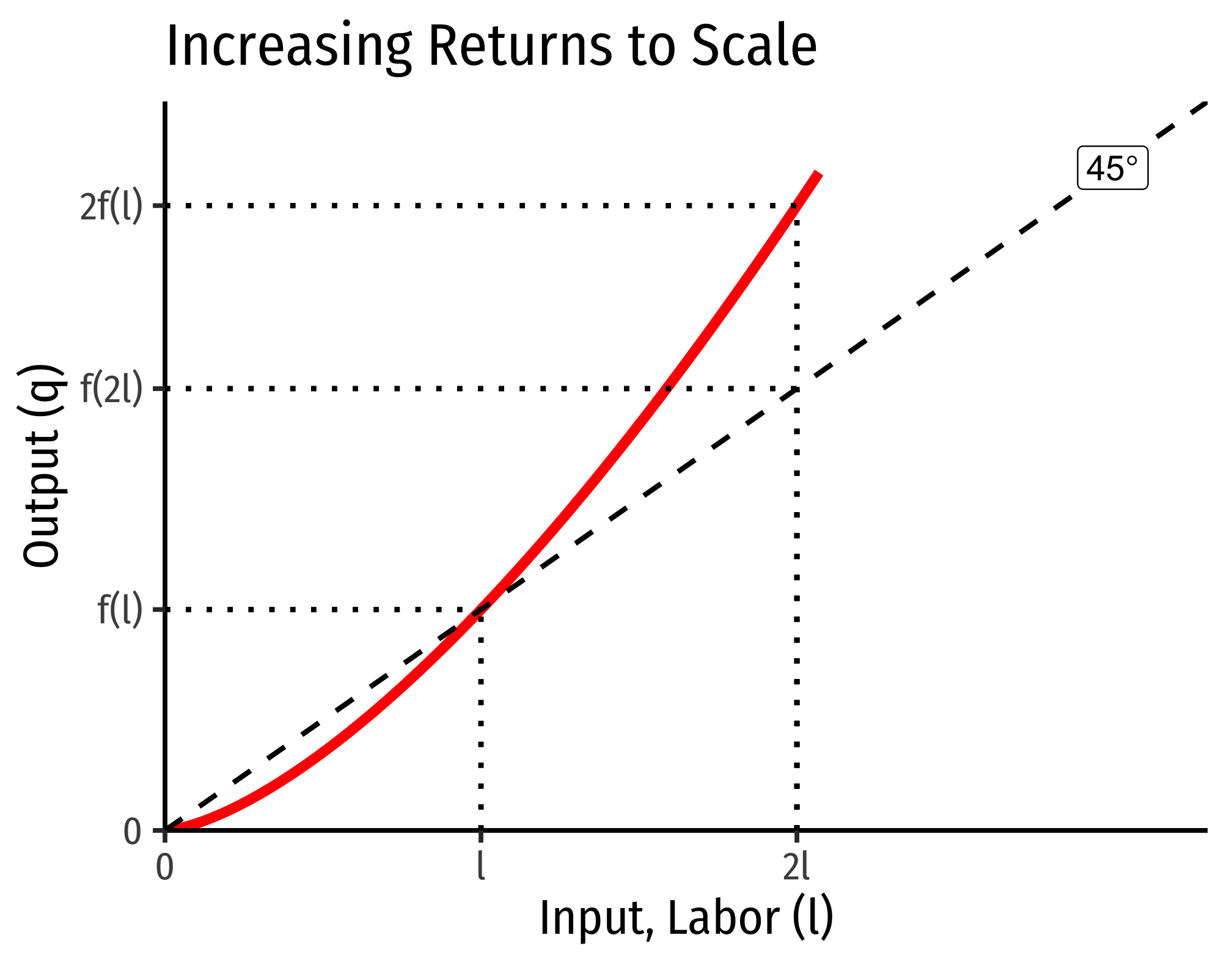
The Relationship Between Returns to Scale and Costs

There is a direct relationship between a technology’s returns to scaleIncreasing, decreasing, or constant

and its cost structure: the rate at which its total costs increaseAt a decreasing rate, at an increasing rate, or at a constant rate, respectively

and its marginal costs changeDecreasing, increasing, or constant, respectively

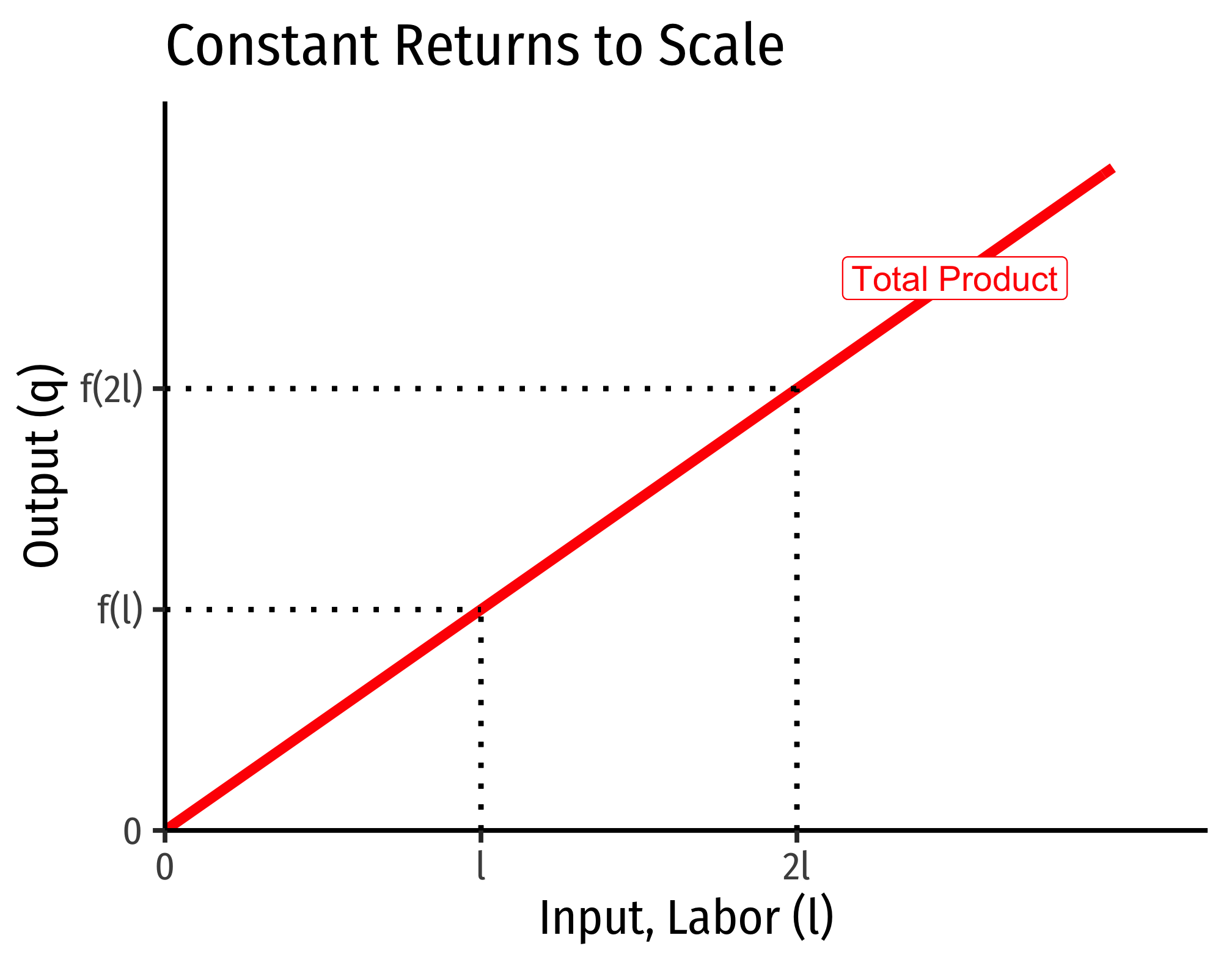
. This is easiest to see for a single input, such as our assumptions of the short run (where firms can change l but not ˉk):

q=f(ˉk,l)

Constant Returns to Scale:

Decreasing Returns to Scale

Increasing Returns to Scale

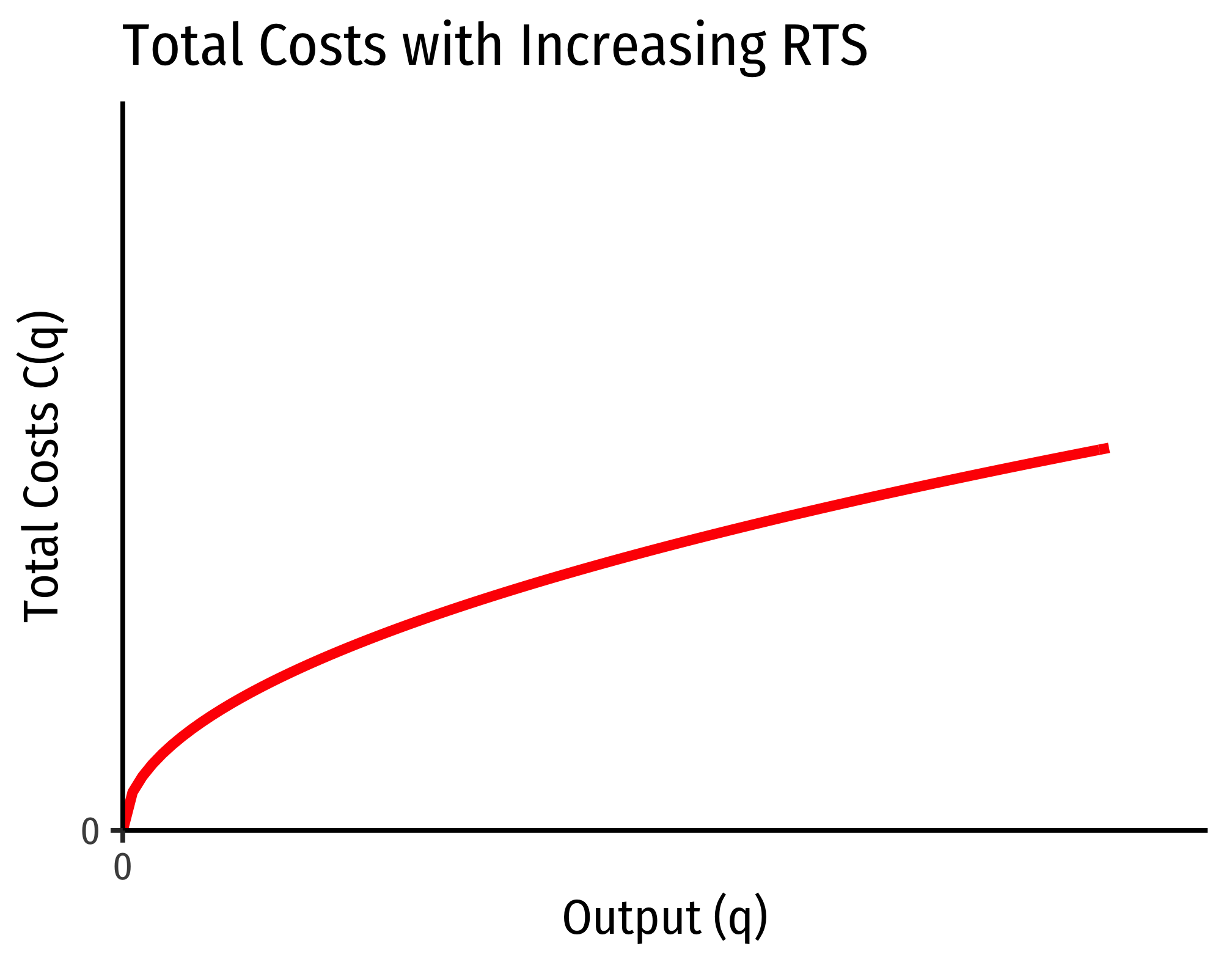
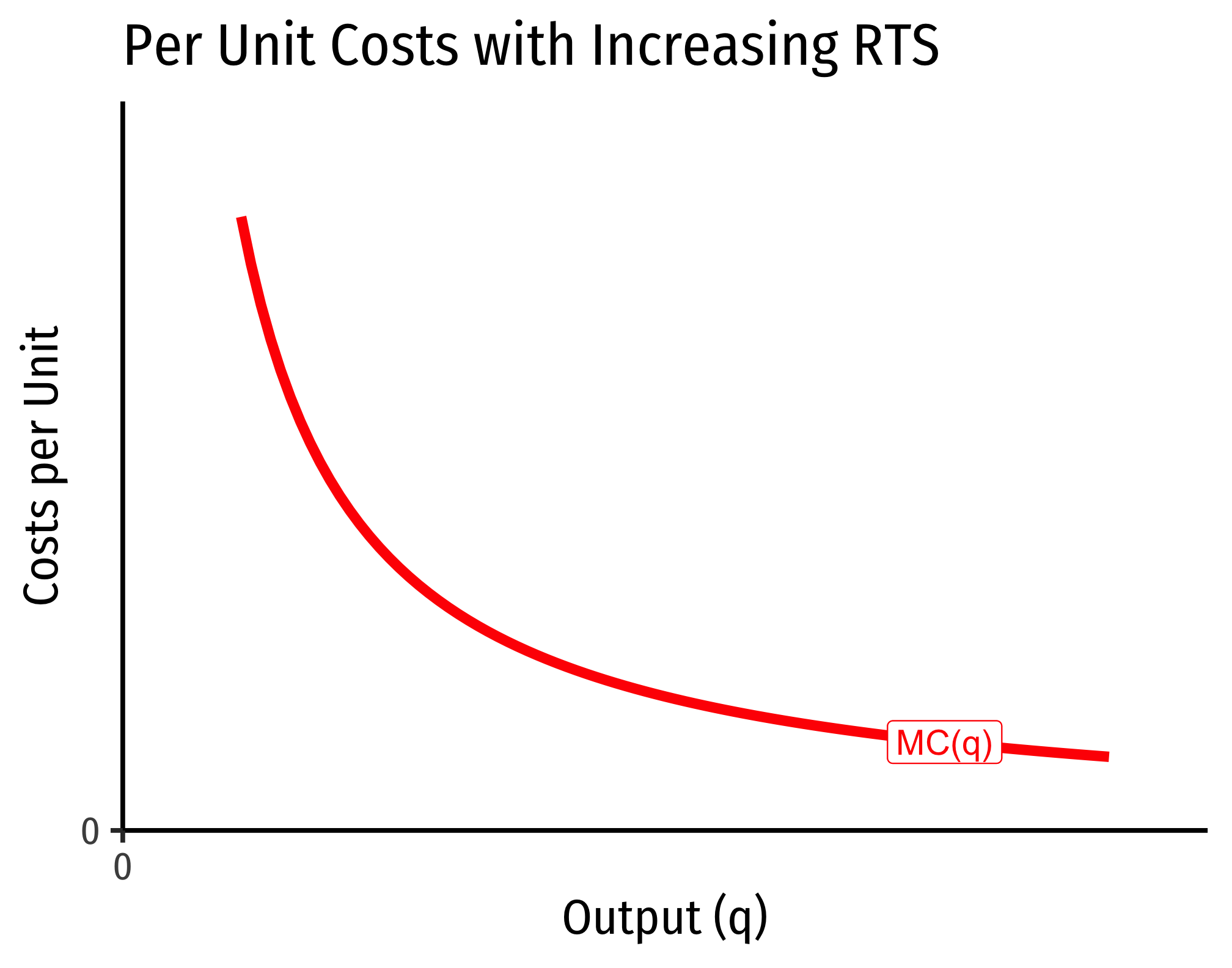
Cobb-Douglas Cost Functions

The total cost function for Cobb-Douglas production functions of the form q=lαkβ

C(w,r,q)=[(αβ)βα+β+(αβ)−αα+β]wαα+βrβα+βq1α+β

If you take the first derivative of this (to get marginal cost), it is:

∂C(w,r,q)∂q=MC(q)=1α+β(wαα+βrβα+β)q(1α+β)−1

How does marginal cost change with increased output? Take the second derivative:

∂2C(w,r,q)∂q2=1α+β(1α+β−1)(wαα+βrβα+β)q(1α+β)−2

• If 1α+β>1, this is positive ⟹ decreasing returns to scale
  • α+β<1 in the production function
• If 1α+β<1, this is negative ⟹ increasing returns to scale
  • α+β>1 in the production function
• If 1α+β=1, this is constant ⟹ constant returns to scale
  • α+β=1 in the production function

Example (Constant Returns)

Let q=l0.5k0.5.

C(w,r,q)=[(0.50.5)0.50.5+0.5+(0.50.5)−0.50.5+0.5]w0.50.5+0.5r0.50.5+0.5q10.5+0.5C(w,r,q)=[10.5+1−0.5]w0.5r0.5q0.5C(w,r,q)=w0.5r0.5q1

If w=9, r=25:

C(w=10,r=20,q)=90.5250.5q=3∗5∗q=15q

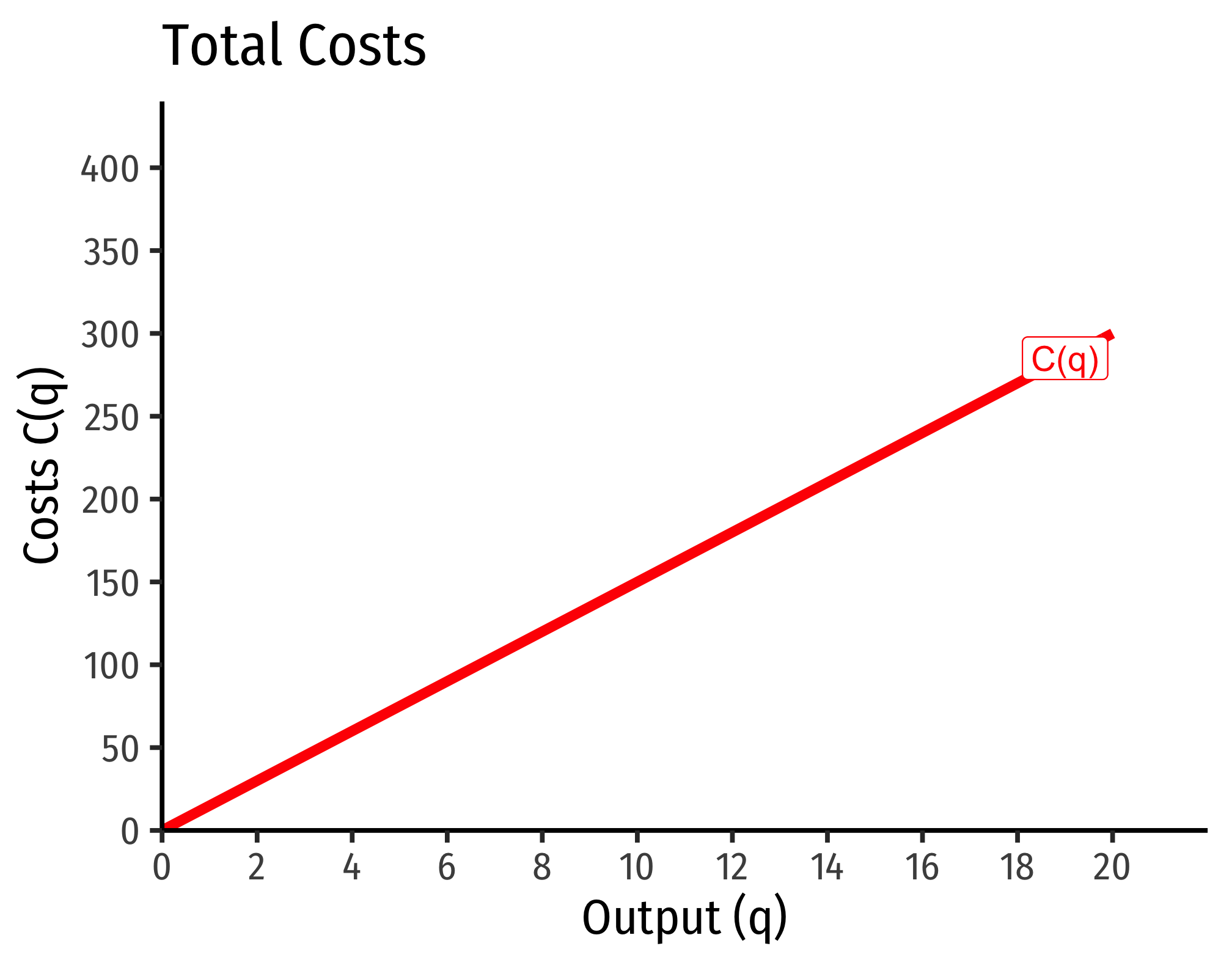
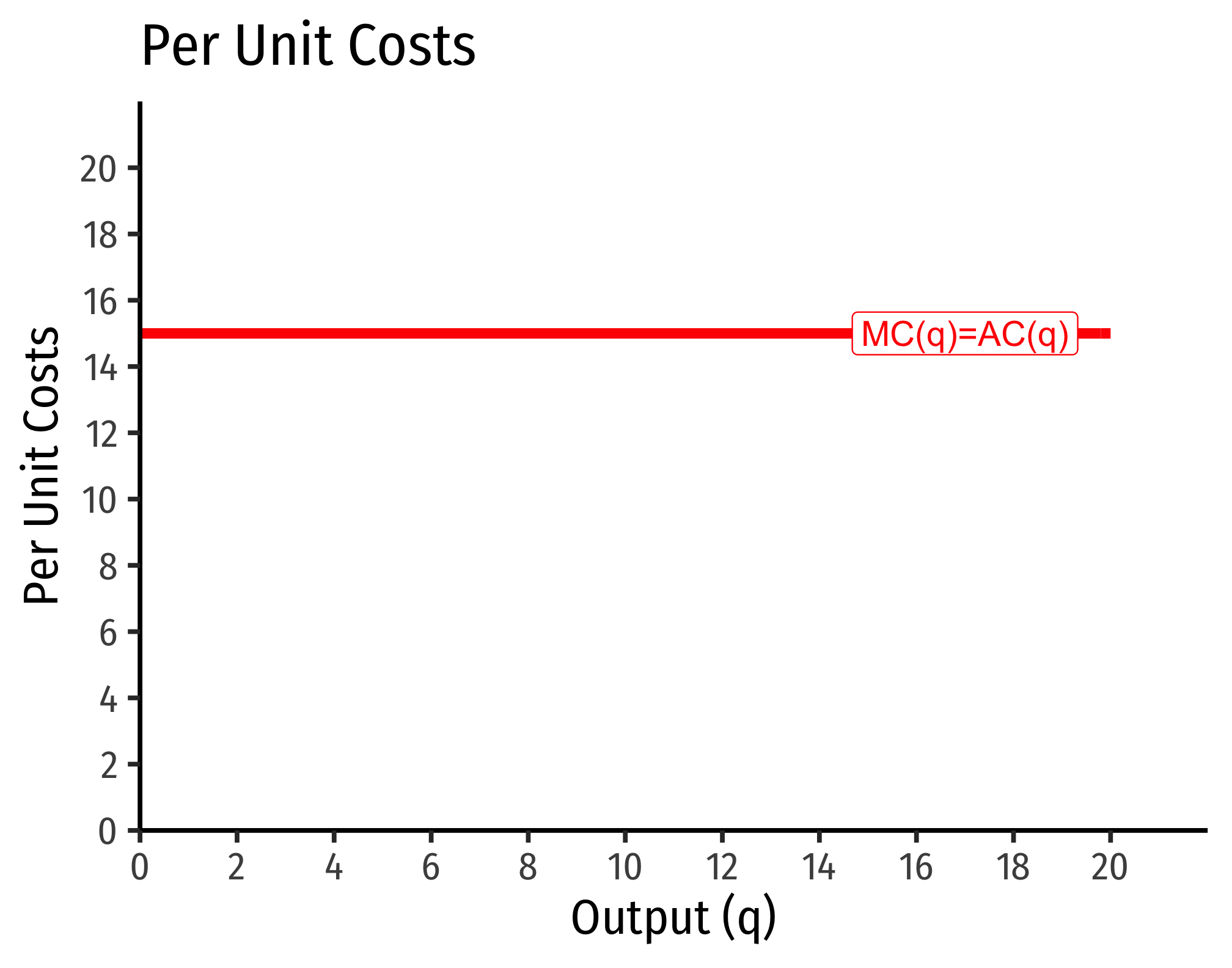
Marginal costs would be

MC(q)=∂C(q)∂q=15

Average costs would be

MC(q)=C(q)q=15qq=15

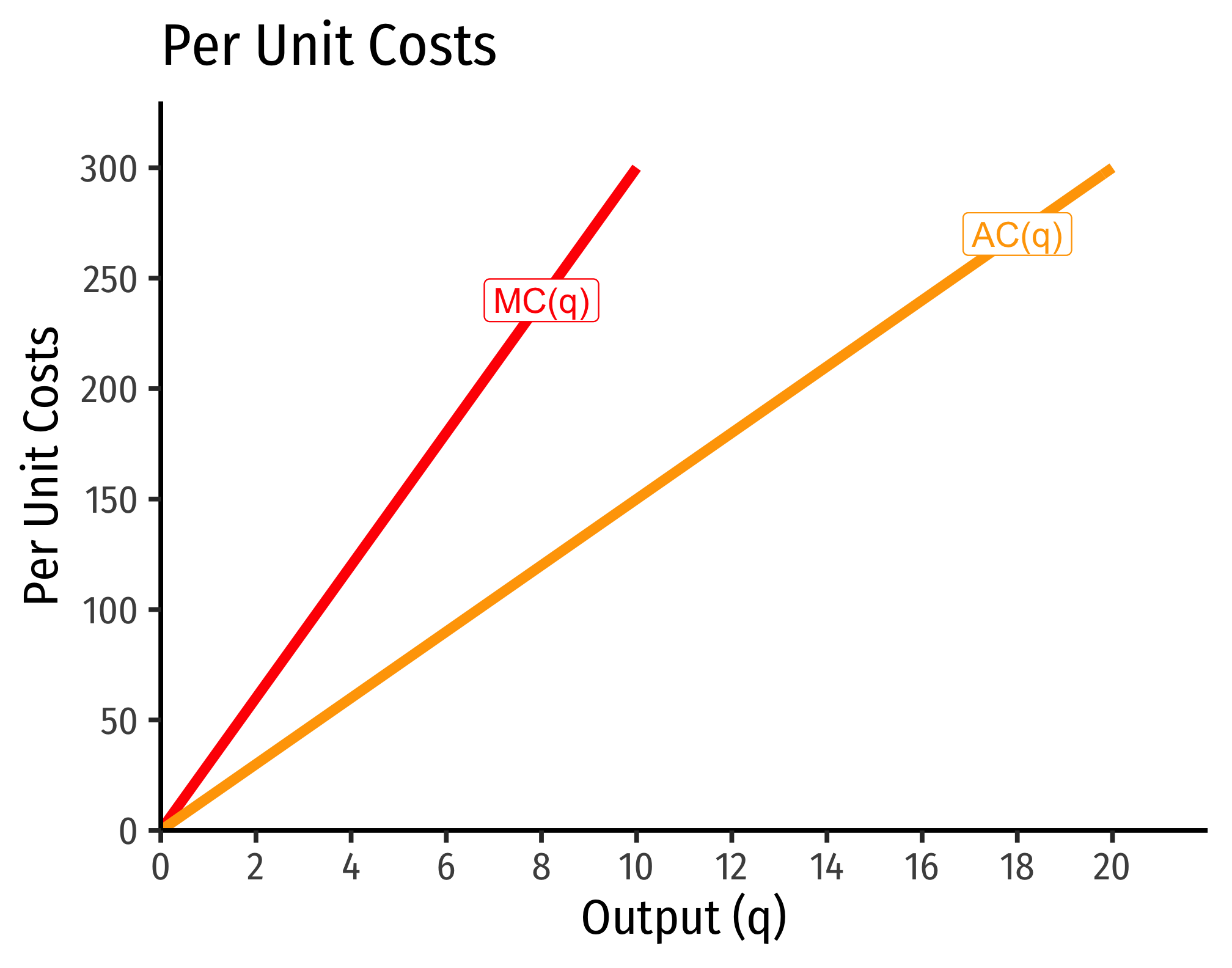
Example (Decreasing Returns)

Let q=l0.25k0.25.

C(w,r,q)=[(0.250.25)0.250.25+0.25+(0.250.25)−0.250.25+0.25]w0.250.25+0.25r0.250.25+0.25q10.25+0.25C(w,r,q)=[10.5+1−0.5]w0.5r0.5q2C(w,r,q)=w0.5r0.5q2

If w=9, r=25:

C(w=10,r=20,q)=90.5250.5q2=3∗5∗q2=15q2

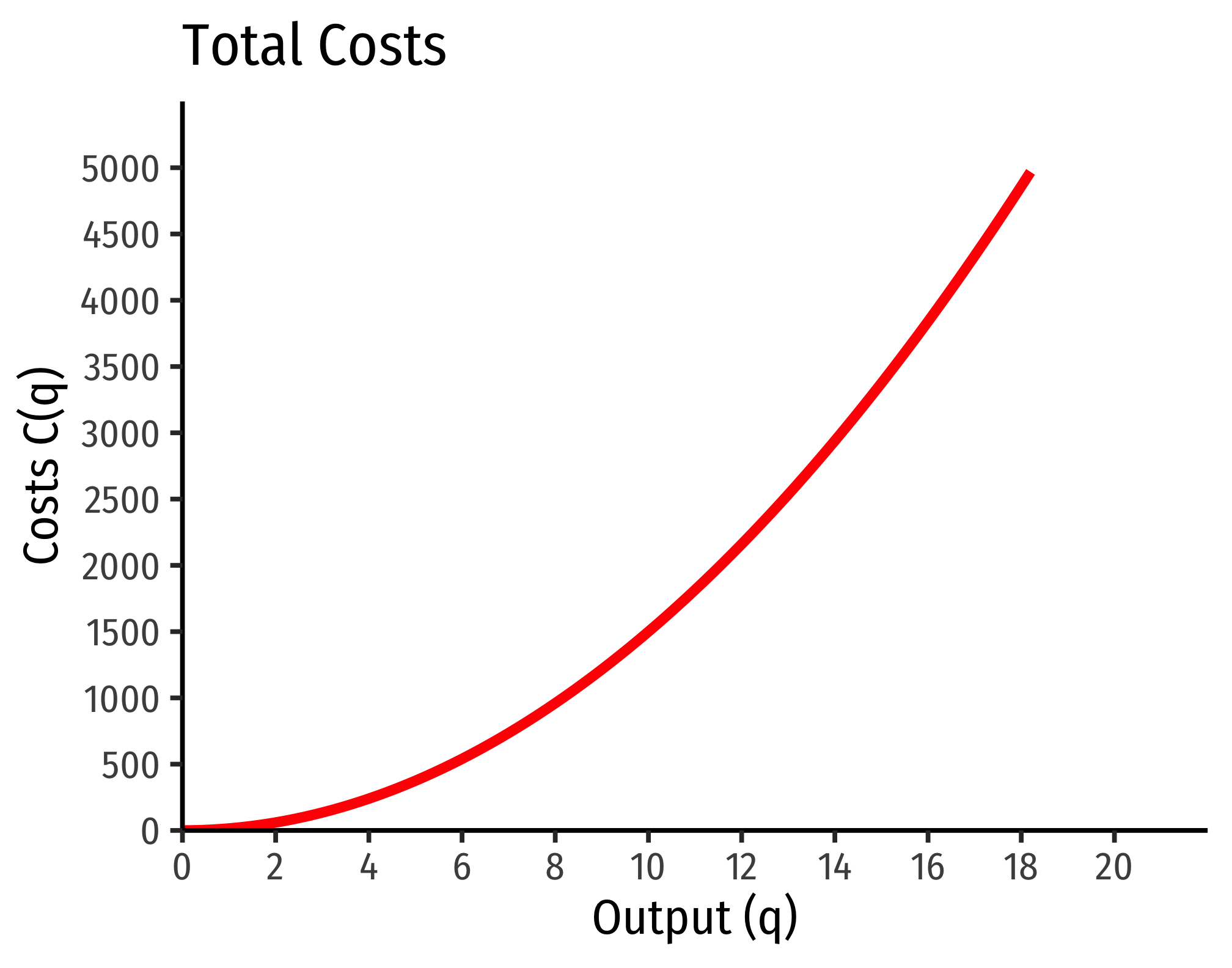
Marginal costs would be

MC(q)=∂C(q)∂q=30q

Average costs would be

AC(q)=C(q)q=15q2q=15q