+ - 0:00:00
Notes for current slide
Notes for next slide

1.7: Deriving a Demand Function

ECON 306 · Microeconomic Analysis · Spring 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microS20
microS20.classes.ryansafner.com

The Consumer's Problem: Review

  • We now can explore the dynamics of how consumers optimally respond to changes in their constraints

  • We know the problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

A Demand Function (for Good X)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?

A Demand Function (for Good X)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income

A Demand Function (for Good X)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)

A Demand Function (for Good X)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)
  3. (Own) Price effects (ΔqDxΔpx): how qDx changes with changes in price (of x)

Income Effect

Income Effect

  • Income effect: change in optimal consumption of a good associated with a change in (nominal) income, holding relative prices constant

ΔqDΔm>?<0

Income Effect (Normal)

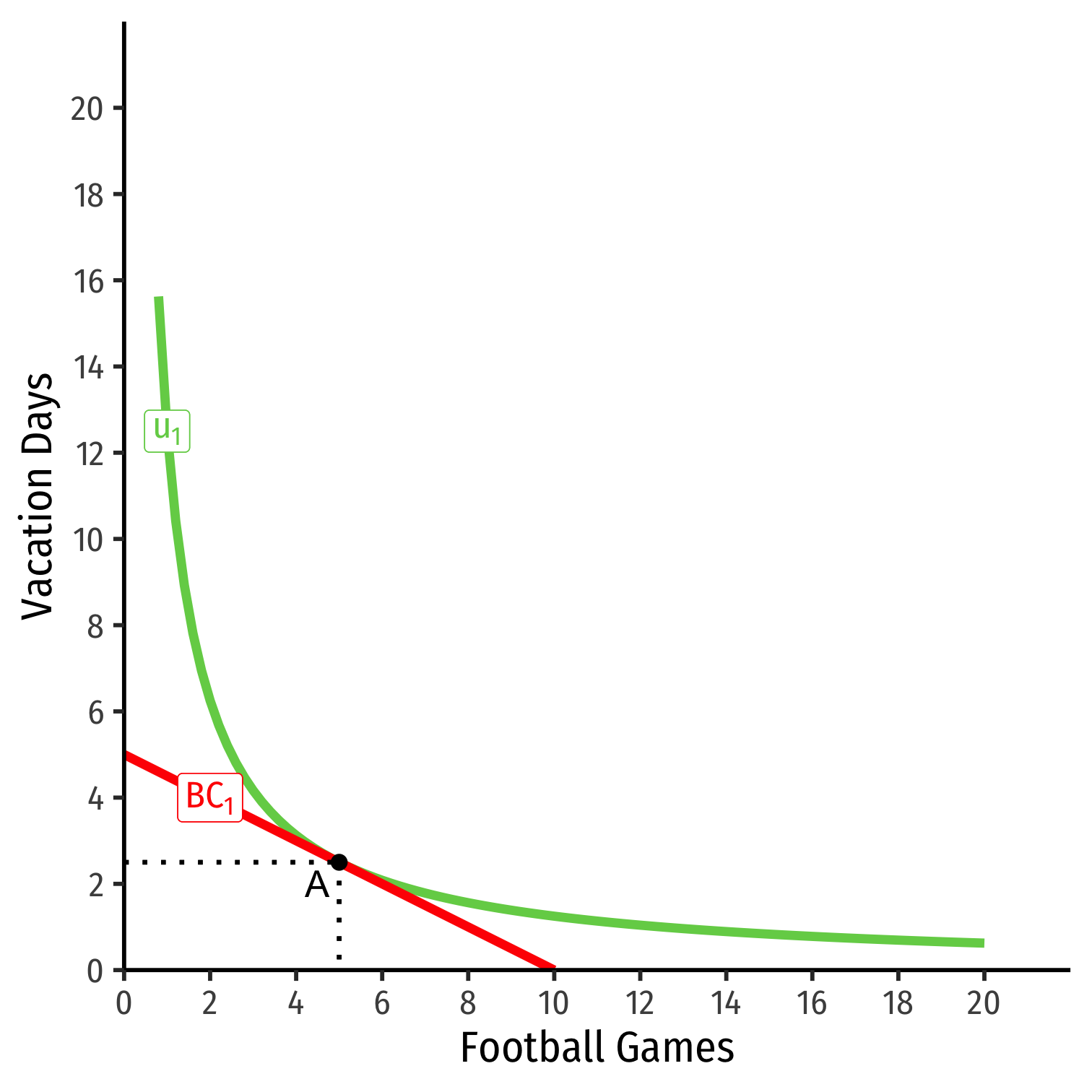
  • Consider football tickets and vacation days

Income Effect (Normal)

  • Consider football tickets and vacation days

  • Suppose income (m) increases

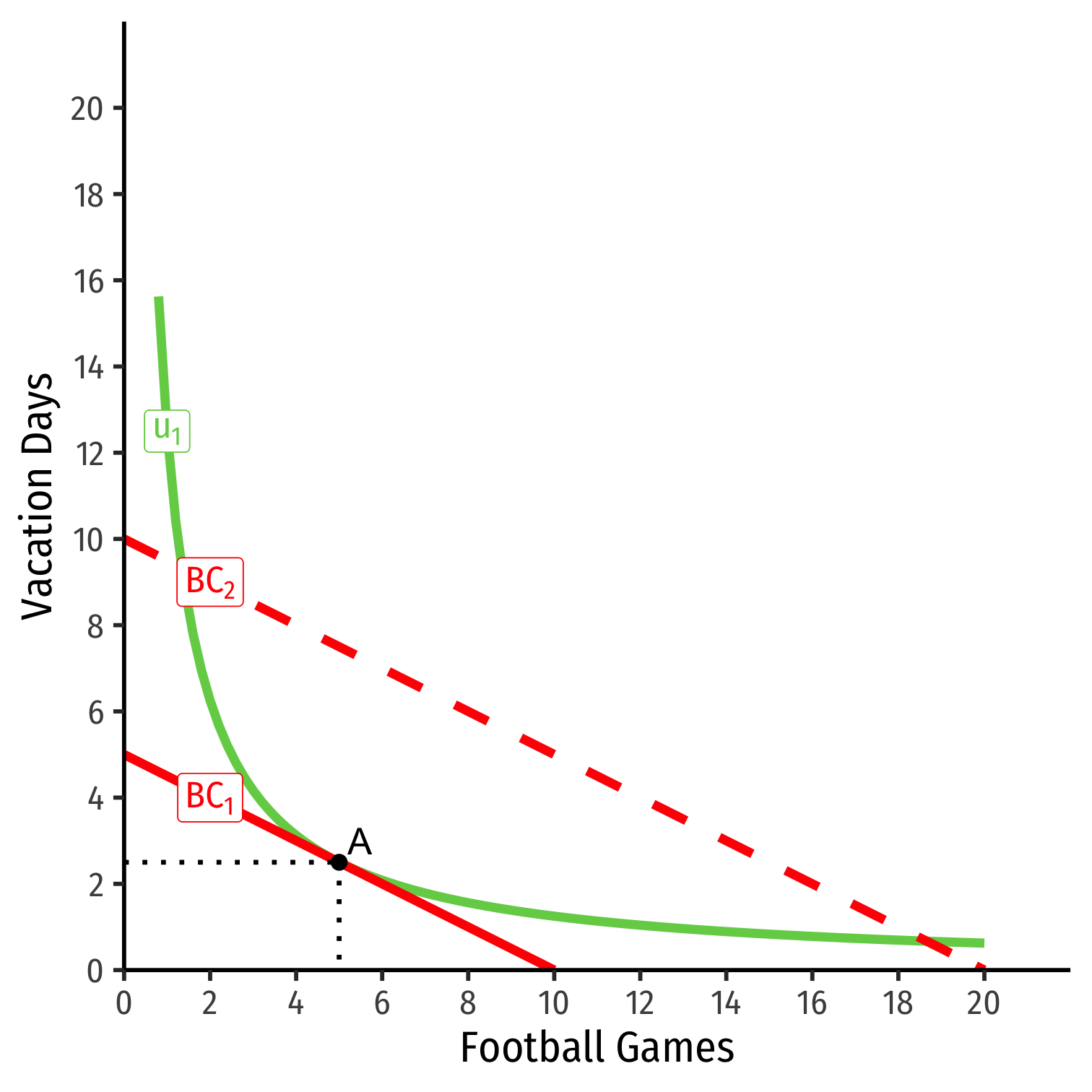
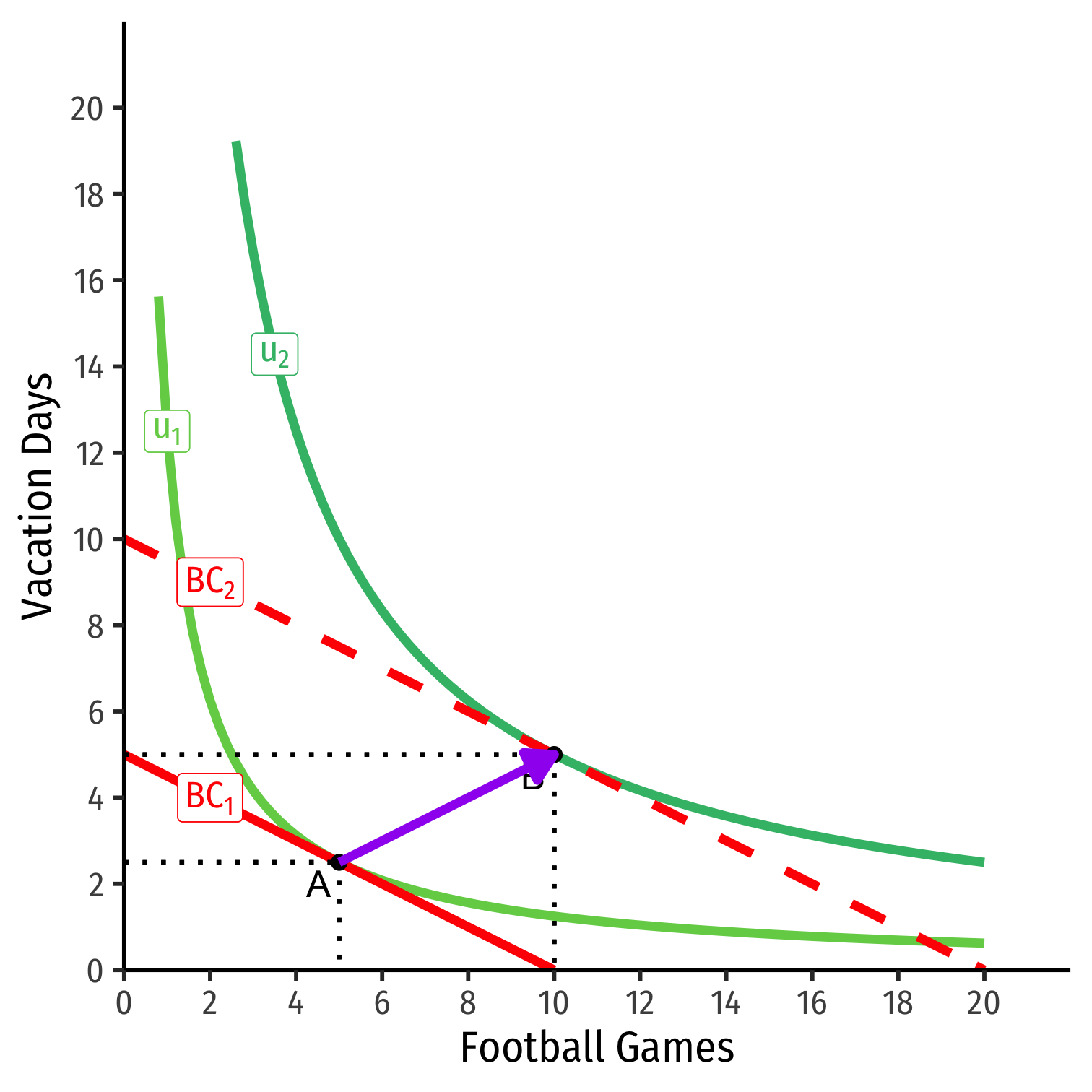
Income Effect (Normal)

  • Consider football tickets and vacation days

  • Suppose income (m) increases

  • At new optimum (B), consumes more of both

  • Then both goods are normal goods

Income Effect (Inferior)

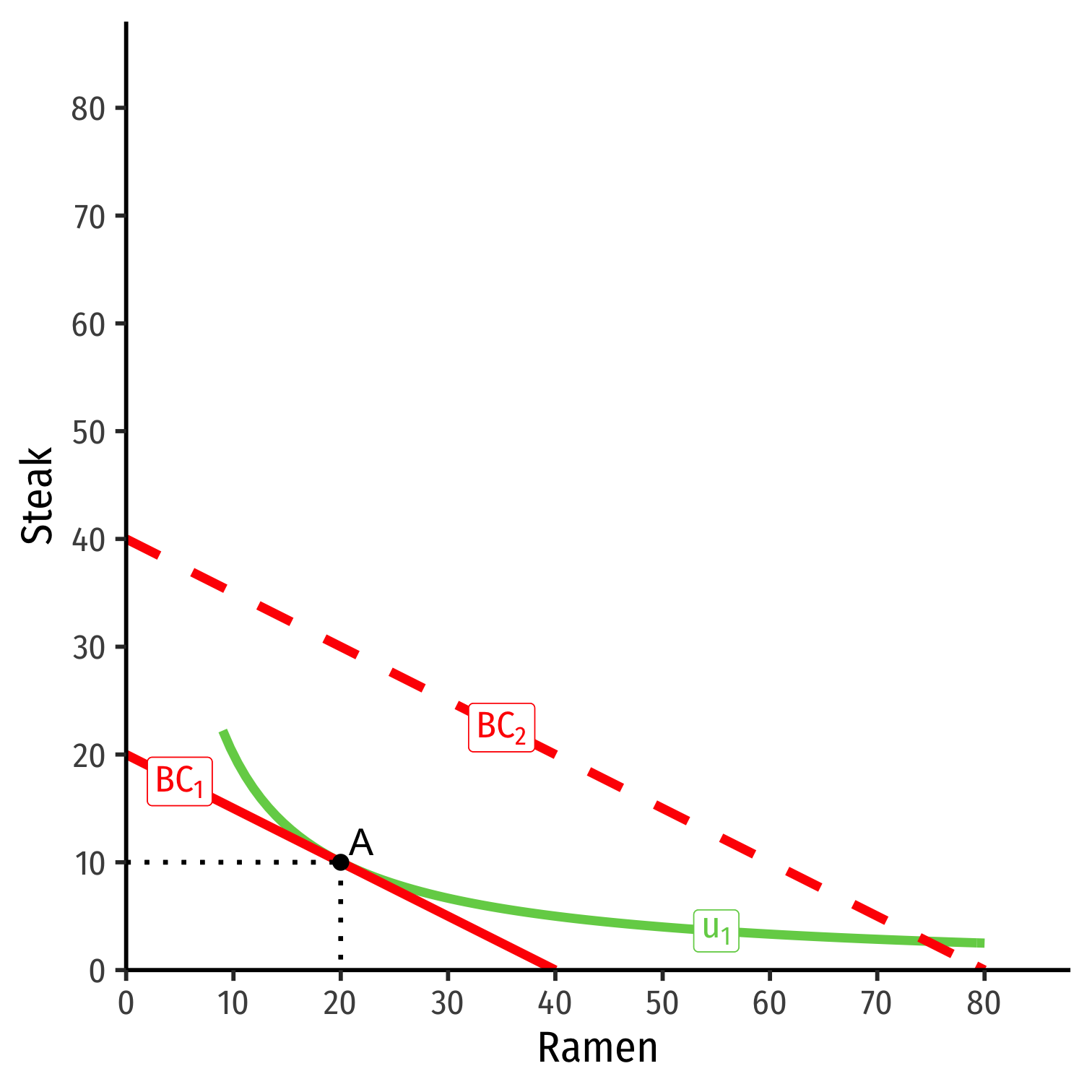
  • Consider ramen and steak

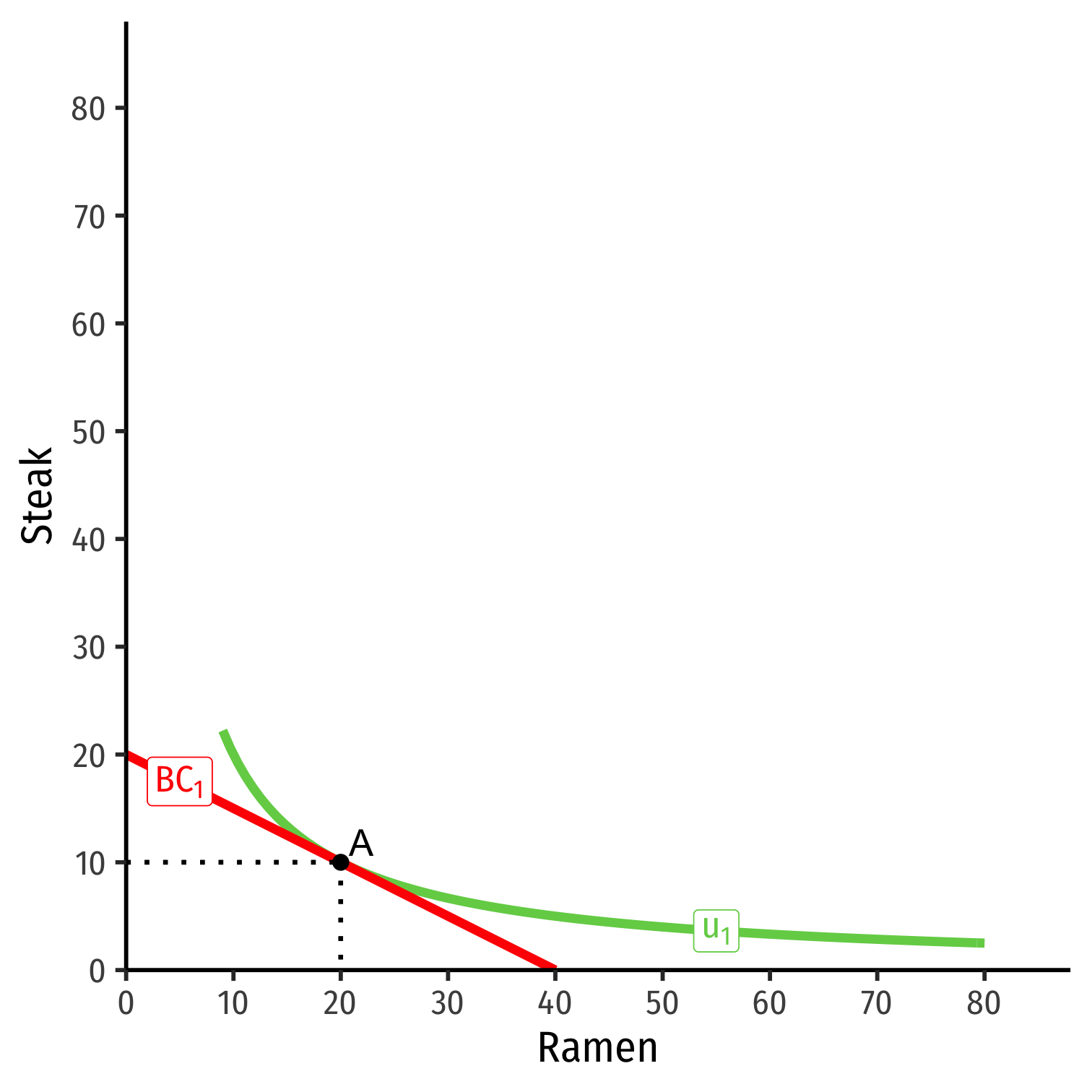
Income Effect (Inferior)

  • Consider ramen and steak

  • Suppose income (m) increases

Income Effect (Inferior)

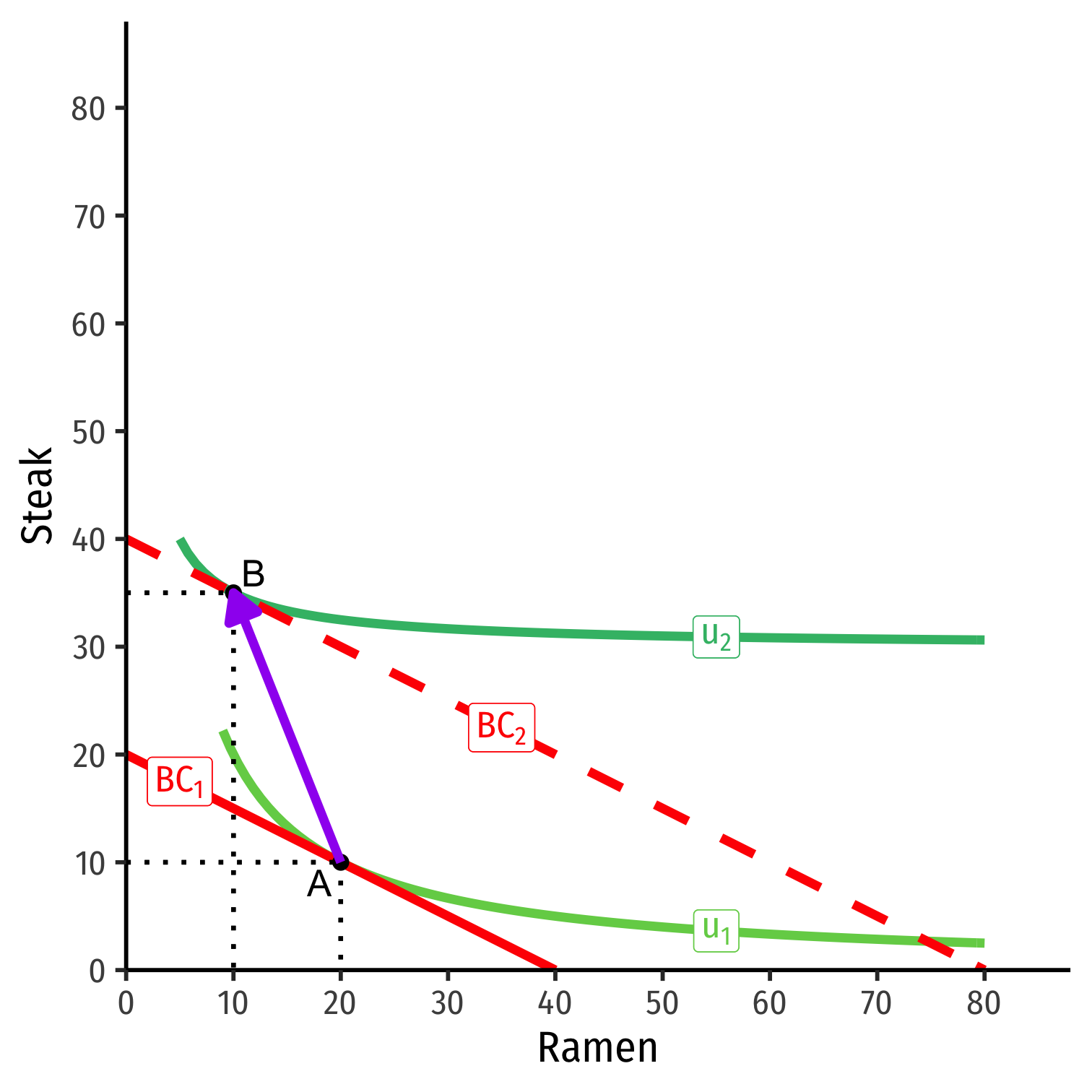
  • Consider ramen and steak

  • Suppose income (m) increases

  • At new optimum (B), consumes more steak, less ramen

  • Steak is a normal good, ramen is an inferior good

Income Effect

ΔqDΔm>?<0

  • Normal goods: consumption increases with more income (and vice versa)

  • Inferior goods: consumption decreases with more income (and vice versa)

Digression: Measuring Change

Quantifying Changes I

  • Several ways we can talk about how a measure changes over time, from time t1→t2

  • Difference (Δ): the difference between the value at time t1 and time t2 Δt=t2−t1

Quantifying Changes II

  • Several ways we can talk about how a measure changes over time, from time t1→t2

  • Difference (Δ): the difference between the value at time t1 and time t2 Δt=t2−t1

  • Relative Difference: the difference expressed in terms of the original value Δtt1=t2−t1t1

    this becomes a proportion (± between 0 and 1)

Quantifying Changes III

  • Several ways we can talk about how a measure changes over time, from time t1→t2

  • Difference (Δ): the difference between the value at time t1 and time t2 Δt=t2−t1

  • Relative Difference: the difference expressed in terms of the original value Δtt1=t2−t1t1

    this becomes a proportion (± between 0 and 1)

Quantifying Changes IV

  • Percentage Change (Growth Rate): relative difference expressed as a percentage (± between 0 and 100%)

%Δ=Δtt1×100%=t2−t1t1×100%

A Simple Example Growth Rate

Example: A country's GDP is $100 in 2019, and $120 in 2020. Calculate the country's GDP growth rate for 2020:

Elasticity, in General

ϵy,x=%Δy%Δx=ΔyyΔxx

  • An elasticity between any two variables y and x describes the responsiveness of a variable (y) to a change in another (x).
    • Relative change of y over the relative change of x

Elasticity, in General

ϵy,x=%Δy%Δx=ΔyyΔxx

  • An elasticity between any two variables y and x describes the responsiveness of a variable (y) to a change in another (x).

    • Relative change of y over the relative change of x

  • Interpretation: ϵy,x= the percentage change in y from a 1% change in x

Elasticity, in General

ϵy,x=%Δy%Δx=ΔyyΔxx

  • An elasticity between any two variables y and x describes the responsiveness of a variable (y) to a change in another (x).

    • Relative change of y over the relative change of x

  • Interpretation: ϵy,x= the percentage change in y from a 1% change in x

  • Unitless: easy comparisons between any 2 variables

    • e.g. crime rates and police, GDP and gov't spending, inequality and corruption

Income Elasticity of Demand I

  • The income elasticity of demand measures how much quantity demanded (qD) changes in response to a change in income (m)

ϵq,m=%ΔqD%Δm

Income Elasticity of Demand I

  • The income elasticity of demand measures how much quantity demanded (qD) changes in response to a change in income (m)

ϵq,m=%ΔqD%Δm

  • If ϵq,m is negative: an inferior good

Income Elasticity of Demand I

  • The income elasticity of demand measures how much quantity demanded (qD) changes in response to a change in income (m)

ϵq,m=%ΔqD%Δm

  • If ϵq,m is negative: an inferior good
  • If ϵq,m is positive: a normal good

Income Elasticity of Demand I

  • The income elasticity of demand measures how much quantity demanded (qD) changes in response to a change in income (m)

ϵq,m=%ΔqD%Δm

  • If ϵq,m is negative: an inferior good
  • If ϵq,m is positive: a normal good
  • Two subtypes of normal goods:
    • Necessity: 0≤ϵq,m≤1
      • ↑ quantity demanded as ↑↑ income (water, clothing)

Income Elasticity of Demand I

  • The income elasticity of demand measures how much quantity demanded (qD) changes in response to a change in income (m)

ϵq,m=%ΔqD%Δm

  • If ϵq,m is negative: an inferior good
  • If ϵq,m is positive: a normal good
  • Two subtypes of normal goods:
    • Necessity: 0≤ϵq,m≤1
      • ↑ quantity demanded as ↑↑ income (water, clothing)
    • Luxury: ϵq,m>1
      • ↑↑ quantity demanded as ↑ income (jewelry, vacations)

Income Elasticity of Demand II

  • For now, we can calculate the income elasticity of demand simply by calculating the relative changes:

%Δq%Δm=(Δqq1)(Δmm1)

  • We'll use some fancier methods when we talk about the only elasticity you've probably seen before: price elasticity of demand

Income Elasticity of Demand: Example

Example: You can spend your income on golf and pancakes. Green fees at a local golf course are $10 per round and pancake mix is $2 per box. When your income is $100, you buy 5 boxes of pancake mix and 9 rounds of golf. When your income increases to $120, you buy 10 boxes of pancake mix and 10 rounds of golf.

  1. What type of good is golf (inferior, necessity, luxury)?

  2. What type of good are pancakes (inferior, necessity, or luxury)?

Income Effects: Example

Example: Is the environment a normal good?

Income Effects: Example

Example: Is the environment a normal good?

Income Effects: Example

Example: Is the environment a normal good?

Income Expansion Path

Goolsbee, et. al (2011: 169)

  • Income expansion path describes how consumption of each good changes when income increases
    • Traces a line between optimal consumption points as income increases (budget constraint shifts out)

Engel Curves

Goolsbee, et. al (2011: 171)

  • Engel curve of each good is more helpful to visualize: shows how consumption of one good changes when income increases

Cross-Price Effects

Cross-Price Effects

  • Cross-price effect: change in optimal consumption of a good associated with a change in price of another good income, holding the good's own price (and income) constant

ΔqxΔpy>?<0

Cross-Price Elasticity of Demand I

  • The cross-price elasticity of demand measures how much quantity demanded of one good (qx) changes in response to a change in price of another good (py)

ϵqx,py=%Δqx%Δpy

Cross-Price Elasticity of Demand I

  • The cross-price elasticity of demand measures how much quantity demanded of one good (qx) changes in response to a change in price of another good (py)

ϵqx,py=%Δqx%Δpy=ΔqxqxΔpypy

Cross-Price Elasticity of Demand II

ϵqx,py=%Δqx%Δpy

  • If ϵqx,py is positive: goods x and y are substitutes

  • An rise (fall) in price of y causes more (less) consumption of x

    • Consumption of x moves in same direction as price of y

Cross-Price Elasticity of Demand III

ϵqx,py=%Δqx%Δpy

  • If ϵqx,py is negative: goods x and y are complements

  • Goods x and y consumed in a bundle, concern about overall price of bundle

  • A rise (fall) in price of y causes less (more) consumption of x

    • Consumption of x moves in opposite direction as price of y

Cross-Price Elasticity: Example I

Example: You can travel into the city every week on Lyft rides and Uber rides. When Lyft is $20/ride, you ride 10 Uber rides. When Lyft raises prices to $25/ride, you ride 15 Uber rides.

  1. What is the relationship between these two goods?

  2. What is the cross-price elasticity?

The Consumer's Problem: Review

  • We now can explore the dynamics of how consumers optimally respond to changes in their constraints

  • We know the problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow