+ - 0:00:00
Notes for current slide
Notes for next slide

2.3: Cost Minimization

ECON 306 · Microeconomic Analysis · Spring 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microS20
microS20.classes.ryansafner.com

Recall: The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

  • 2nd Stage: firm's cost minimization problem:

  1. Choose: < inputs >

  2. In order to minimize: < cost >

  3. Subject to: < producing the optimal output >

  • Minimizing costs ⟺ maximizing profits

Solving the Cost Minimization Problem

The Firm's Cost Minimization Problem

  • The firm's cost minimization problem is:

  1. Choose: < inputs: l,k>

  2. In order to maximize: < total cost: wl+rk >

  3. Subject to: < producing the optimal output: q∗=f(l,k) >

The Cost Minimization Problem: Tools

  • Our tools for firm's input choices:

  • Choice: combination of inputs (l,k)

  • Production function/isoquants: firm's technological constraints

    • How the firm trades off between inputs
  • Isocost line: firm's total cost (for given output and input prices)
    • How the market trades off between inputs

The Cost Minimization Problem: Verbally

  • The firms's cost minimization problem:

choose a combination of l and k to minimize total cost that produces the optimal amount of output

The Cost Minimization Problem: Math

minl,kwl+rk

s.t.q∗=f(l,k)

  • This requires calculus to solve. We will look at graphs instead!

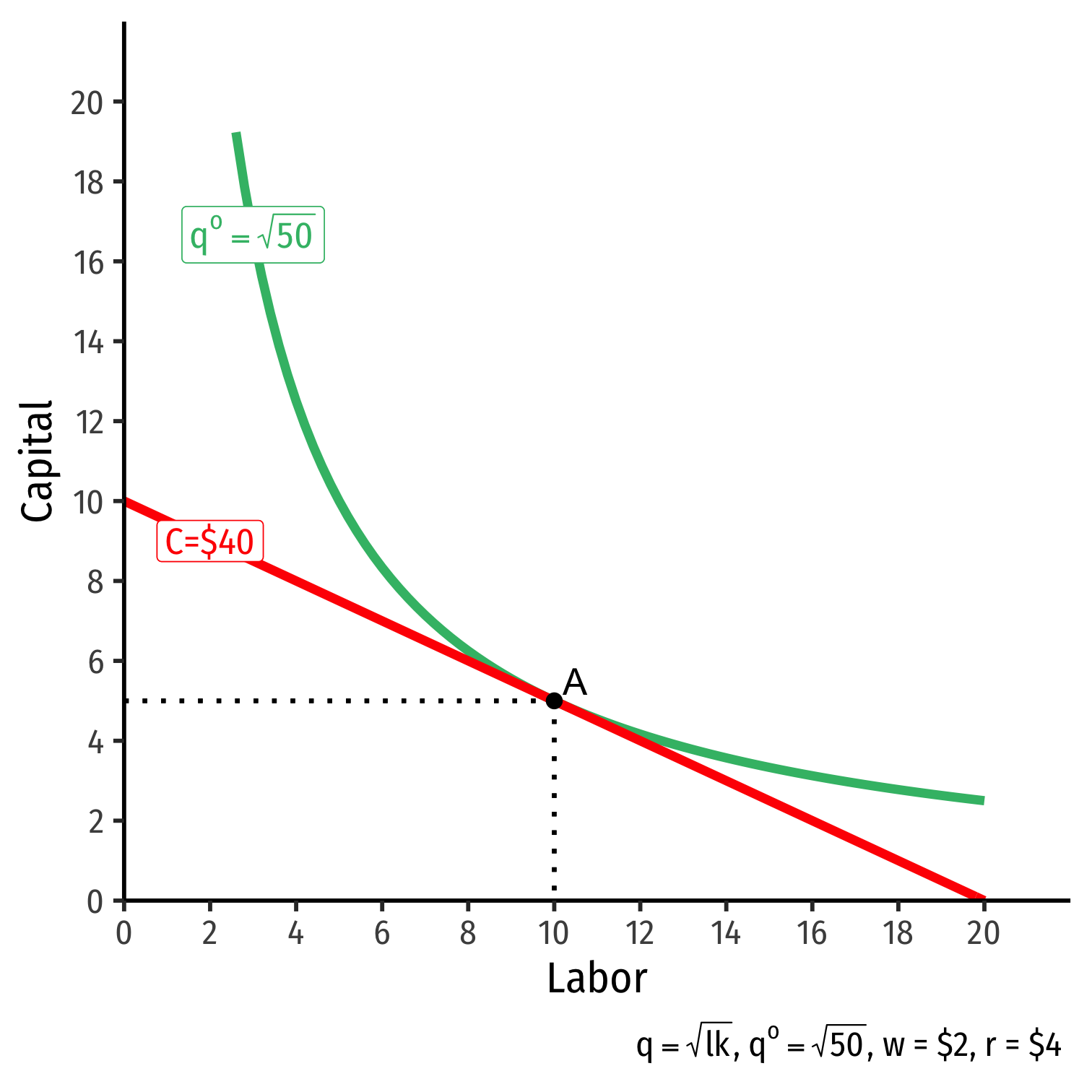
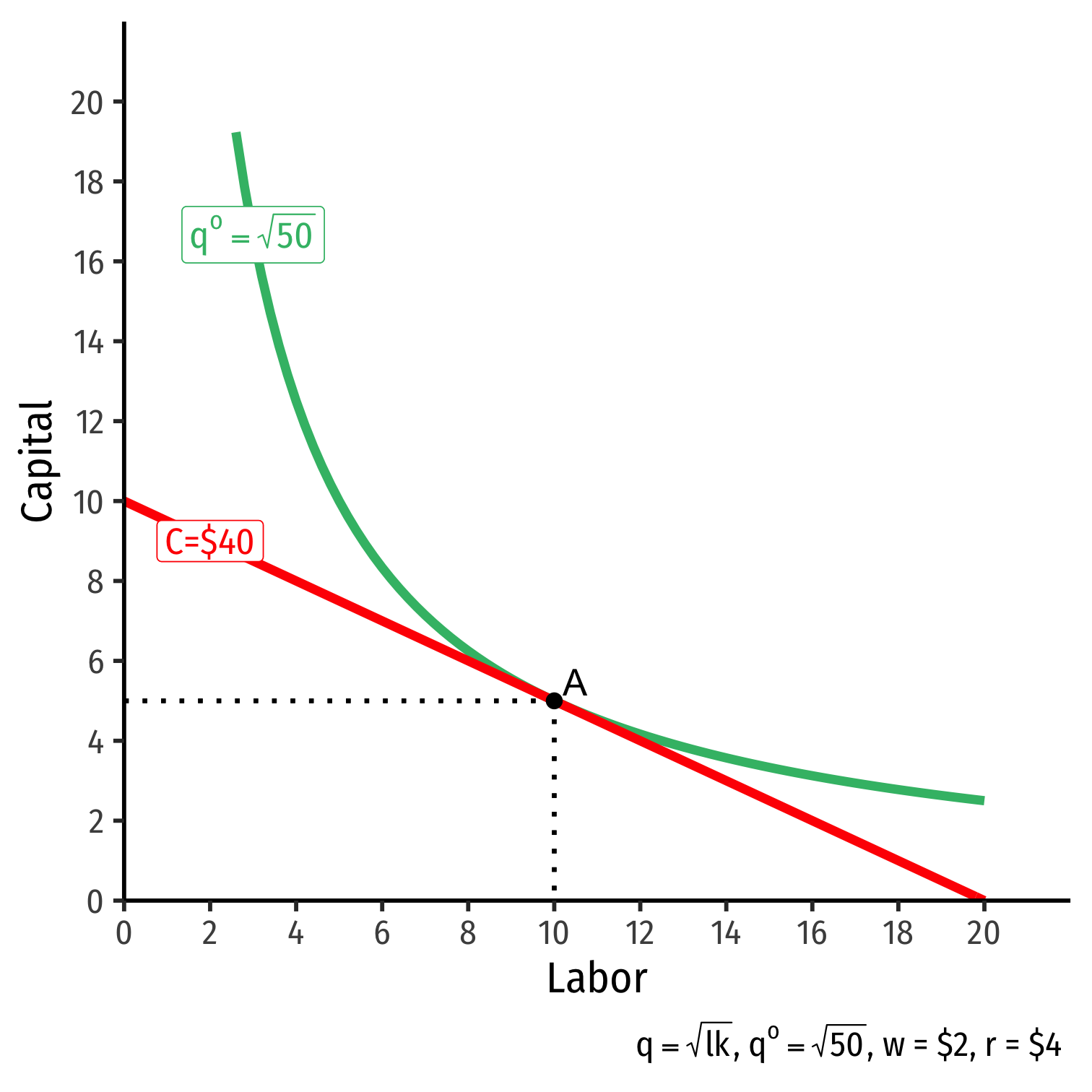
The Firm's Least-Cost Input Combination: Graphically

  • Graphical solution: Lowest isocost line tangent to desired isoquant (A)

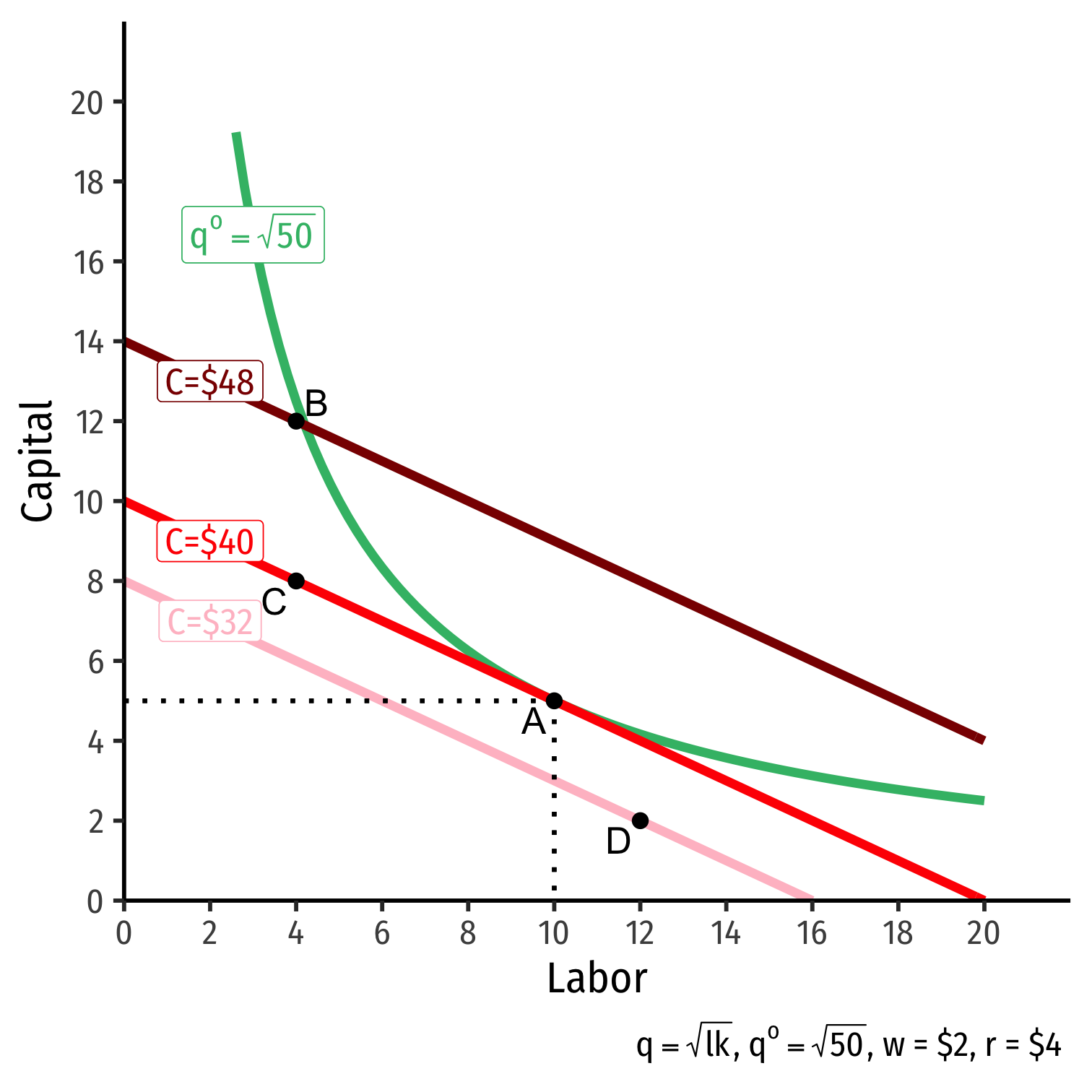
The Firm's Least-Cost Input Combination: Graphically

  • Graphical solution: Lowest isocost line tangent to desired isoquant (A)

  • B produces same output as A, but higher cost

  • C is same cost as A, but produces less than desired output

  • D produces is cheaper, but produces less than desired output

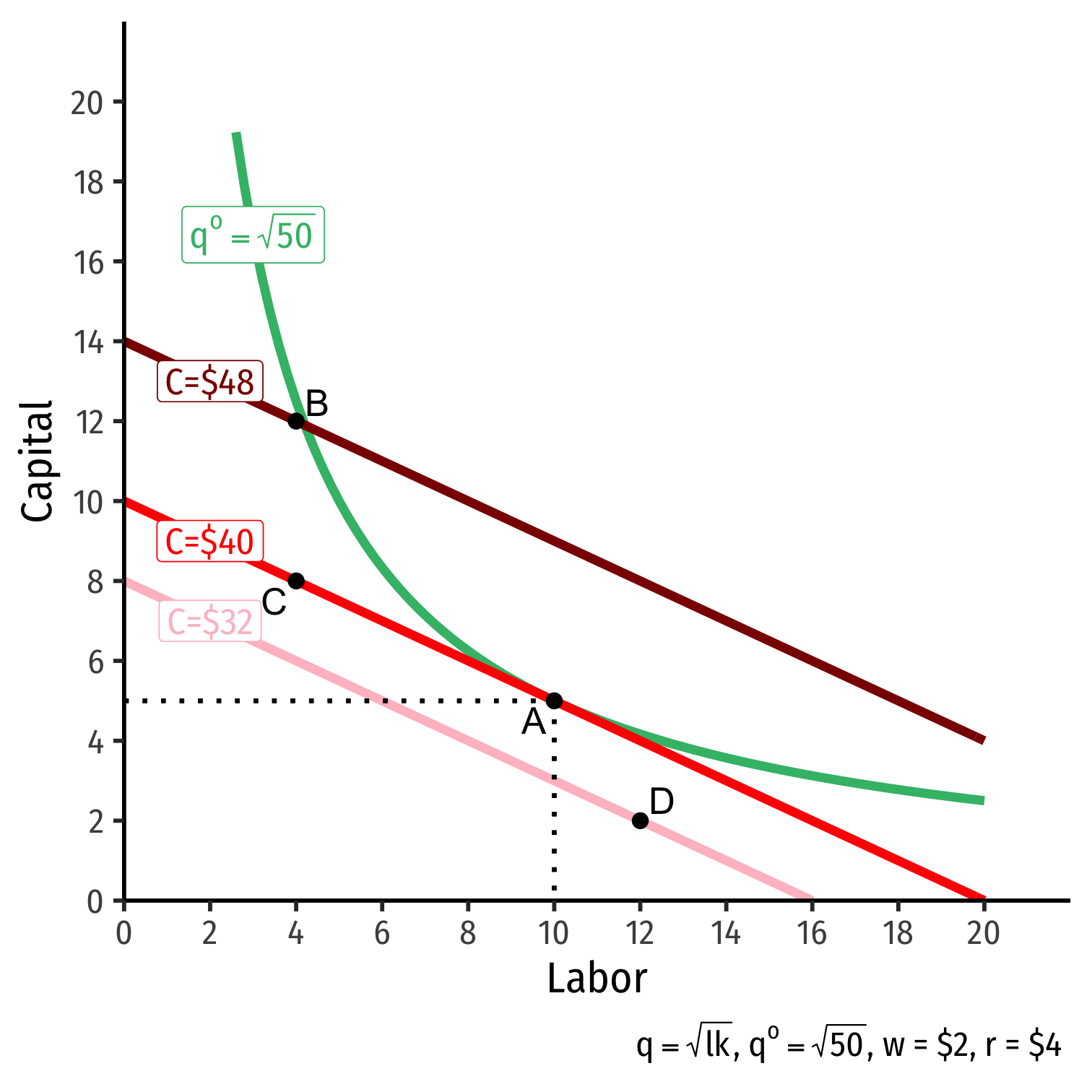
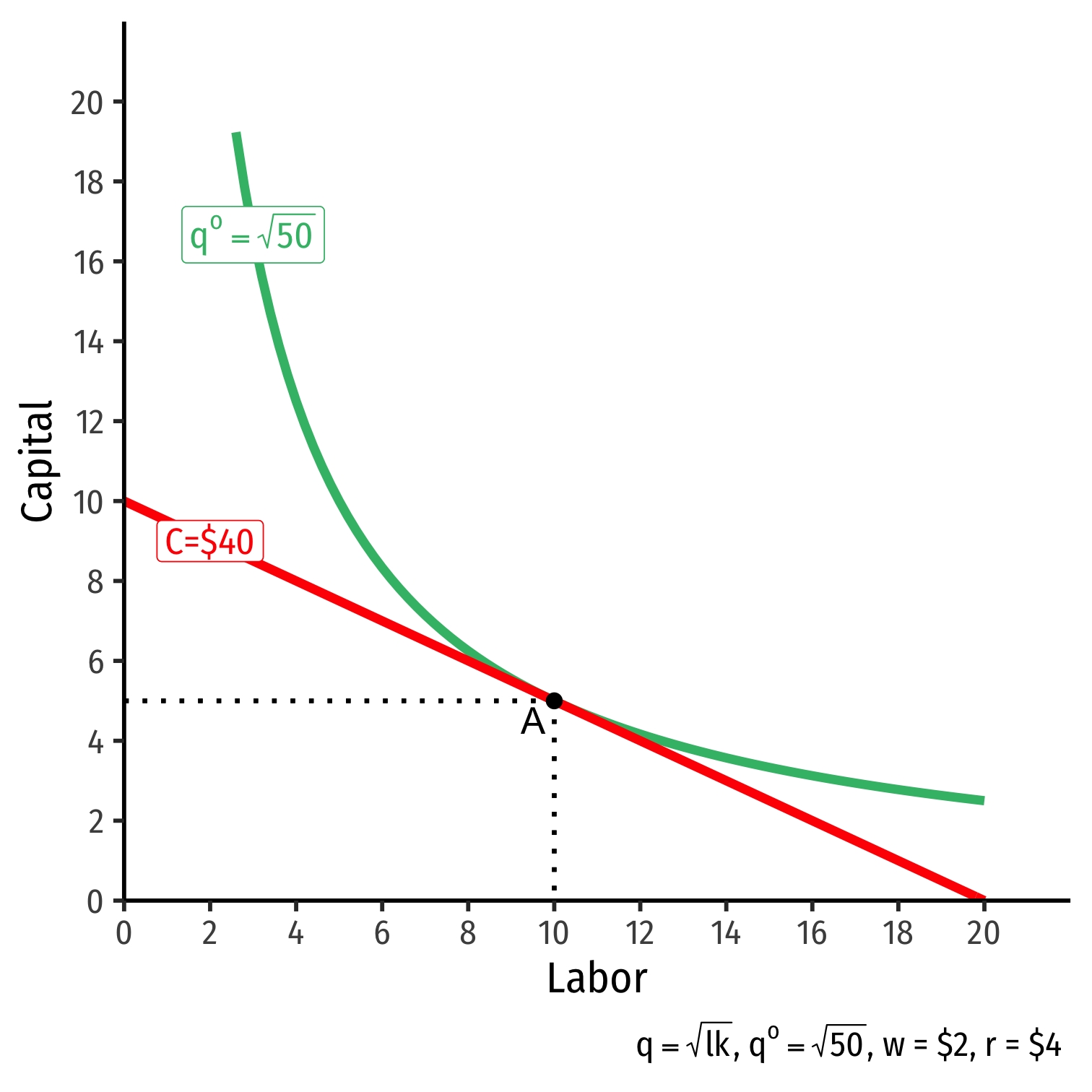
The Firm's Least-Cost Input Combination: Why A?

Isoquant curve slope=Isocost line slope

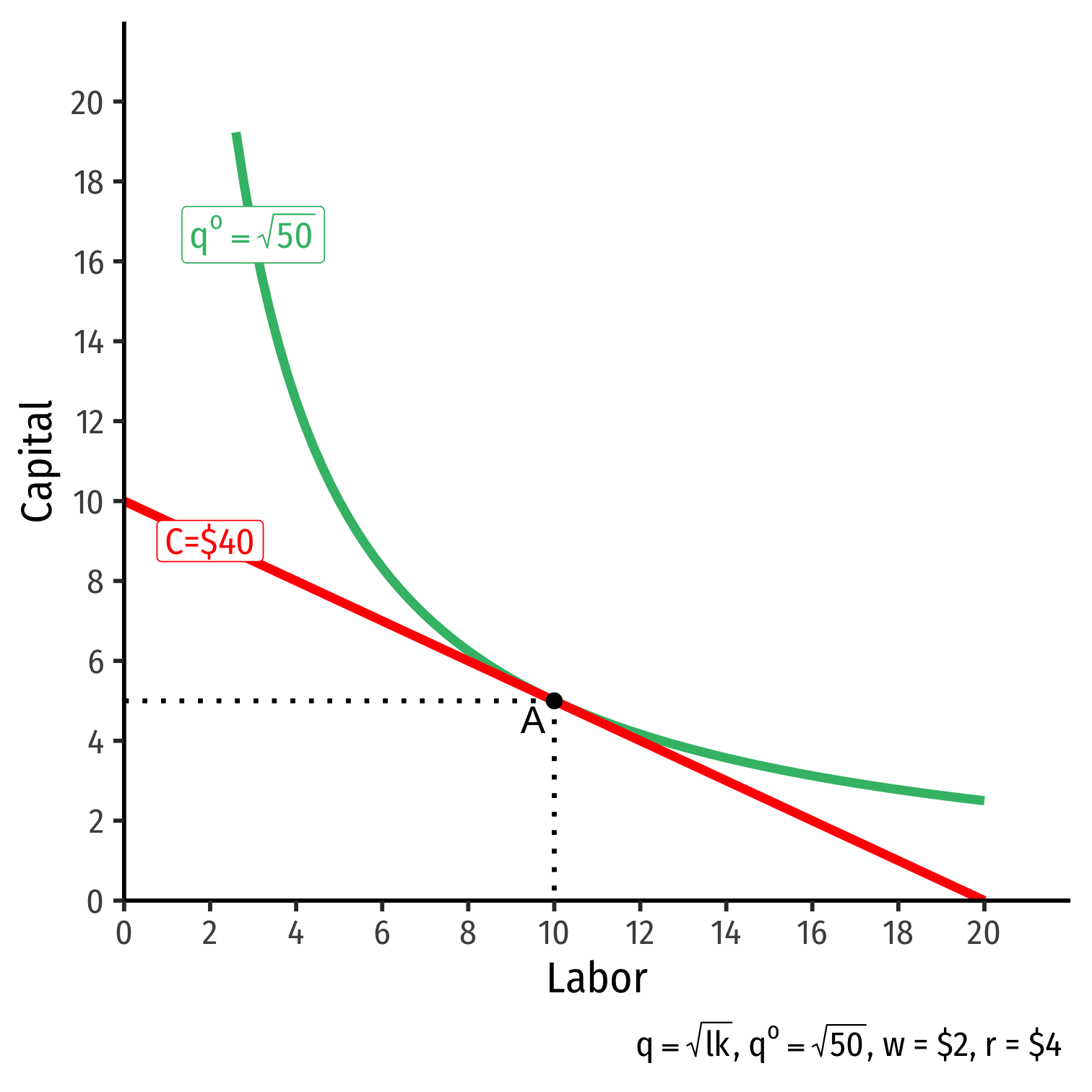
The Firm's Least-Cost Input Combination: Why A?

Isoquant curve slope=Isocost line slope|MRTSl,k|=|wr||MPlMPk|=|wr||−0.5|=|−0.5|

  • Firm would exchange at same rate as market

  • No other combination of (l,k) exists at current prices & output that could lower cost to produce q∗!

Two Equivalent Rules

Rule 1

MPlMPk=wr

  • Easier for solving math problems

Two Equivalent Rules

Rule 1

MPlMPk=wr

  • Easier for solving math problems

Rule 2

MPlw=MPkr

  • Easier for intuition (next slide)

The Equimarginal Rule Again I

MPlw=MPkr=⋯=MPnpn

  • Equimarginal Rule: the cost of production is minimized where the marginal product per dollar spent is equalized across all n possible inputs

  • Firm will always choose an option that gives higher marginal product (e.g. if MPl>MPk)

    • But each option has a different cost, so we weight each option by its cost, hence MPnpn

The Equimarginal Rule Again II

MPlw=MPkr=⋯=MPnpn

  • Why is this the optimum?

  • Example: suppose firm could get a higher marginal product per $1 spent on l than for k (i.e. "more bang for your buck"!)

    • Not minimizing costs!
    • Should use more l and less k!
      • This will raise MPk and lower MPl!
    • Continue until cost-adjusted marginal products are equalized

The Equimarginal Rule Again III

  • Any optimum in economics: no better alternatives exist under current constraints

  • No possible change in your inputs to produce q∗ that would lower cost

The Firm's Least-Cost Input Combination: Example

Example:

Your firm can use labor l and capital k to produce output according to the production function: q=2lk

The marginal products are:

MPl=2kMPk=2l

You want to produce 100 units, the price of labor is $10, and the price of capital is $5.

  1. What is the least-cost combination of labor and capital that produces 100 units of output?
  2. How much does this combination cost?

Returns to Scale

Returns to Scale

  • The returns to scale of production refers to the change in output when all inputs are increased at the same rate

Returns to Scale

  • The returns to scale of production refers to the change in output when all inputs are increased at the same rate

  • Constant returns to scale: output increases at same proportionate rate as inputs increase

    • e.g. if you double all inputs, output doubles

Returns to Scale

  • The returns to scale of production refers to the change in output when all inputs are increased at the same rate

  • Constant returns to scale: output increases at same proportionate rate as inputs increase

    • e.g. if you double all inputs, output doubles
  • Increasing returns to scale: output increases more than proportionately to the change in inputs
    • e.g. if you double all inputs, output more than doubles

Returns to Scale

  • The returns to scale of production refers to the change in output when all inputs are increased at the same rate

  • Constant returns to scale: output increases at same proportionate rate as inputs increase

    • e.g. if you double all inputs, output doubles
  • Increasing returns to scale: output increases more than proportionately to the change in inputs
    • e.g. if you double all inputs, output more than doubles
  • Decreasing returns to scale: output increases less than proportionately to the change in inputs
    • e.g. if you double all inputs, output less than doubles

Returns to Scale: Example

Example: Does each of the following production functions exhibit constant returns to scale, increasing returns to scale, or decreasing returns to scale?

  1. q=4l+2k

  2. q=2lk

  3. q=2l0.3k0.3

Returns to Scale: Cobb-Douglas

  • One reason we often use Cobb-Douglas production functions is to easily determine returns to scale:
    q=Akαlβ

  • α+β=1: constant returns to scale

  • α+β>1: increasing returns to scale
  • α+β<1: decreasing returns to scale
  • Note this trick only works for Cobb-Douglas functions!

Cobb-Douglas: Constant Returns Case

  • In the constant returns to scale case (most common), Cobb-Douglas is often written as:
    q=Akαl1−α

  • α is the output elasticity of capital

    • A 1% increase in k leads to a α% increase in q

  • 1−α is the output elasticity of labor

    • A 1% increase in l leads to a (1−α)% increase in q

Output-Expansion Paths & Cost Curves

Goolsbee et. al (2011: 246)

  • Output Expansion Path: curve illustrating the changes in the optimal mix of inputs and the total cost to produce an increasing amount of output

  • Total Cost curve: curve showing the total cost of producing different amounts of output (next class)

  • See next class' notes page to see how we go from our least-cost combinations over a range of outputs to derive a total cost function

Recall: The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

  • 2nd Stage: firm's cost minimization problem:

  1. Choose: < inputs >

  2. In order to minimize: < cost >

  3. Subject to: < producing the optimal output >

  • Minimizing costs ⟺ maximizing profits

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow